99. Recover Binary Search Tree

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

You are given the root of a binary search tree (BST), where exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Example 1:

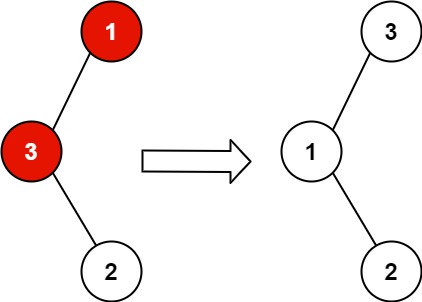
Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

Example 2:

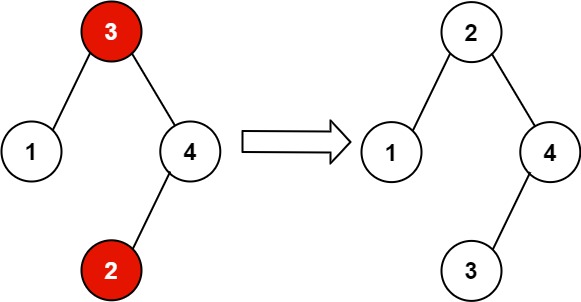
Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.

Constraints:

• The number of nodes in the tree is in the range $[2, 1000]$.
• $-2^{31} <= Node.val <= 2^{31} - 1$

Follow up: A solution using O(n) space is pretty straight-forward. Could you devise a constant O(1) space solution?

Code

recursion

class Solution {
    // 第一个错误值
    TreeNode first = null;
    // 第二个错误值
    TreeNode second = null;
    // 之前的节点
    TreeNode prev = null;
    public void recoverTree(TreeNode root) {
        if(root == null) return;

        // 找到first和second
        helper(root);

        int temp = first.val;
        first.val = second.val;
        second.val = temp;
    }
    // 中序遍历
    private void helper(TreeNode root){
        if(root == null) return;

        helper(root.left);
        // 出现了错误的值，中序遍历之前的值比之后的值大
        if(prev != null && prev.val >= root.val){
            // 有两个数顺序不对
            // 第一个错误是prev
            // 第二个错误是root
            // [1,(3),(2),4,5]
            // [1,(4),3,(2),5]
            if(first == null) first = prev;
            second = root;
        }
        prev = root;
        helper(root.right);
    }
}

stack

class Solution {
    public void recoverTree(TreeNode root) {
        if(root == null) return;
        TreeNode first = null;
        TreeNode second = null;
        TreeNode prev = null;

        TreeNode curr = root;
        Stack<TreeNode> stack = new Stack<>();
        while(!stack.isEmpty() || curr != null){
            if(curr != null){
                stack.push(curr);
                curr = curr.left;
            } else{
                curr = stack.pop();
                if(prev != null && prev.val >= curr.val){
                    if(first == null) first = prev;
                    second = curr;
                }

                prev = curr;
                curr = curr.right;
            }
        }

        int temp = first.val;
        first.val = second.val;
        second.val = temp;
    }
}