655. Print Binary Tree

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:

• The height of the tree is height and the number of rows m should be equal to height + 1.
• The number of columns n should be equal to $2^{height+1} - 1$.
• Place the root node in the middle of the top row (more formally, at location $res[0][(n-1)/2]$).
• For each node that has been placed in the matrix at position res[r][c], place its left child at $res[r+1][c-2^{height-r-1}]$ and its right child at $res[r+1][c+2^{height-r-1}]$.
• Continue this process until all the nodes in the tree have been placed.
• Any empty cells should contain the empty string “”.

Return the constructed matrix res.

Example 1:

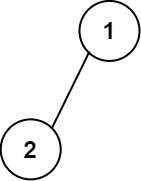
Input: root = [1,2]
Output:
[["","1",""],
 ["2","",""]]

Example 2:

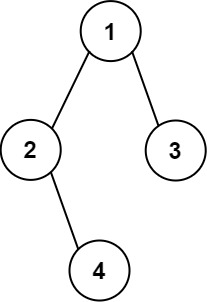
Input: root = [1,2,3,null,4]
Output:
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]

Constraints:

• The number of nodes in the tree is in the range $[1, 2^{10}]$.
• -99 <= Node.val <= 99
• The depth of the tree will be in the range [1, 10].

Code

314. Binary Tree Vertical Order Traversal

class Solution {
    public List<List<String>> printTree(TreeNode root) {
        int height = getHeight(root);

        List<List<String>> res = new ArrayList<>();
        List<String> row = new ArrayList<>();

        for(int i = 0; i < Math.pow(2, height) - 1; i++) {
            row.add("");
        }

        for(int i = 0; i < height; i++) {
            res.add(new ArrayList<>(row));
        }

        helper(res, root, (int)((Math.pow(2, height) - 1) / 2), 0, height);
        return res;
    }

    private void helper(List<List<String>> res, TreeNode curr, int col, int row, int height) {
        if(curr == null) return;

        res.get(row).set(col, curr.val + "");

        int nextRow = row + 1;
        int diff = (int)(Math.pow(2, height - nextRow - 1));
        helper(res, curr.left, col - diff, nextRow, height);
        helper(res, curr.right, col + diff, nextRow, height);
    }

    private int getHeight(TreeNode root) {
        if(root == null) return 0;
        return 1 + Math.max(getHeight(root.left), getHeight(root.right));
    }
}