JIAKAOBO

LeetCode

venmo
wechat

感谢赞助!

  • ㊗️
  • 大家
  • offer
  • 多多！

Problem

You are given two integers height and width representing a garden of size height x width. You are also given:

  • an array tree where tree = [tree_r, tree_c] is the position of the tree in the garden,
  • an array squirrel where squirrel = [squirrel_r, squirrel_c] is the position of the squirrel in the garden,
  • and an array nuts where nuts[i] = [nut_ir, nut_ic] is the position of the ith nut in the garden.

The squirrel can only take at most one nut at one time and can move in four directions: up, down, left, and right, to the adjacent cell.

Return the minimal distance for the squirrel to collect all the nuts and put them under the tree one by one.

The distance is the number of moves.

Example 1:

img

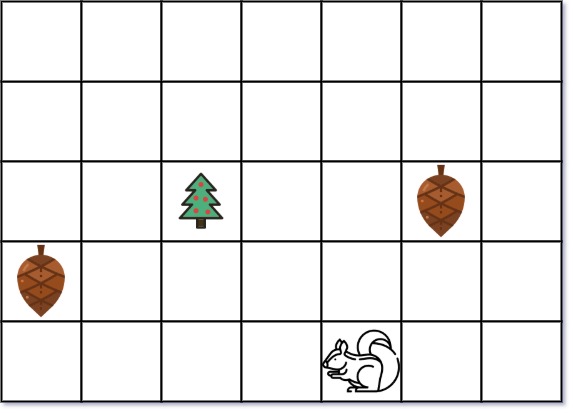
Input: height = 5, width = 7, tree = [2,2], squirrel = [4,4], nuts = [[3,0], [2,5]]
Output: 12
Explanation: The squirrel should go to the nut at [2, 5] first to achieve a minimal distance.

Example 2:

img

Input: height = 1, width = 3, tree = [0,1], squirrel = [0,0], nuts = [[0,2]]
Output: 3

Constraints:

  • 1 <= height, width <= 100
  • tree.length == 2
  • squirrel.length == 2
  • 1 <= nuts.length <= 5000
  • nuts[i].length == 2
  • $0 <= tree_r, squirrel_r, nut_ir <= height$
  • $0 <= tree_c, squirrel_c, nut_ic <= width$

Code

class Solution {
    public int minDistance(int height, int width, int[] tree, int[] squirrel, int[][] nuts) {
        int sum = 0;
        int maxDiff = - (width + height);
        
        for (int[] nut : nuts) {
            int tree2nut = Math.abs(tree[0] - nut[0]) + Math.abs(tree[1] - nut[1]);
            sum += 2 * tree2nut;
            
            int squ2nut = Math.abs(squirrel[0] - nut[0]) + Math.abs(squirrel[1] - nut[1]);
            maxDiff = Math.max(maxDiff, tree2nut - squ2nut);
        }
        
        return sum - maxDiff;
    }
}