538. Convert BST to Greater Tree

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.

As a reminder, a binary search tree is a tree that satisfies these constraints:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

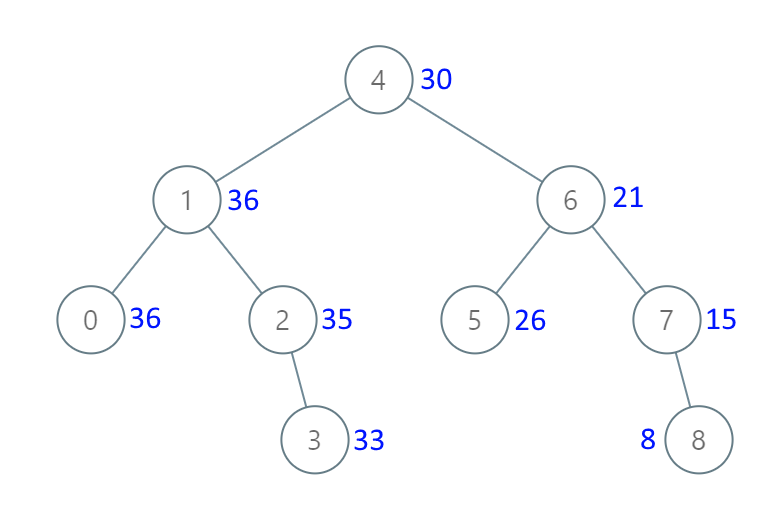
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

Input: root = [0,null,1]
Output: [1,null,1]

Constraints:

• The number of nodes in the tree is in the range [0, 10^4].
• -10^4 <= Node.val <= 10^4
• All the values in the tree are unique.
• root is guaranteed to be a valid binary search tree.

Note: This question is the same as 1038

Code

重复题目 1038

class Solution {
    int sum = 0;

    public TreeNode convertBST(TreeNode root) {
        if (root == null) return null;
        
        convertBST(root.right);
        
        sum += root.val;
        root.val = sum;
        
        convertBST(root.left);
        
        return root;
    }
}

class Solution {
    public TreeNode convertBST(TreeNode root) {
        int sum = 0;
        TreeNode node = root;
        Stack<TreeNode> stack = new Stack<>();

        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                stack.add(node);
                node = node.right;
            }

            node = stack.pop();
            sum += node.val;
            node.val = sum;

            node = node.left;
        }

        return root;
    }
}