518. Coin Change II

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

The answer is guaranteed to fit into a signed 32-bit integer.

Example 1:

Input: amount = 5, coins = [1,2,5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

Input: amount = 10, coins = [10]
Output: 1

Constraints:

• 1 <= coins.length <= 300
• 1 <= coins[i] <= 5000
• All the values of coins are unique.
• 0 <= amount <= 5000

Code

322. Coin Change 377. Combination Sum IV 416. Partition Equal Subset Sum

amount = 5, coins = [1,2,5]

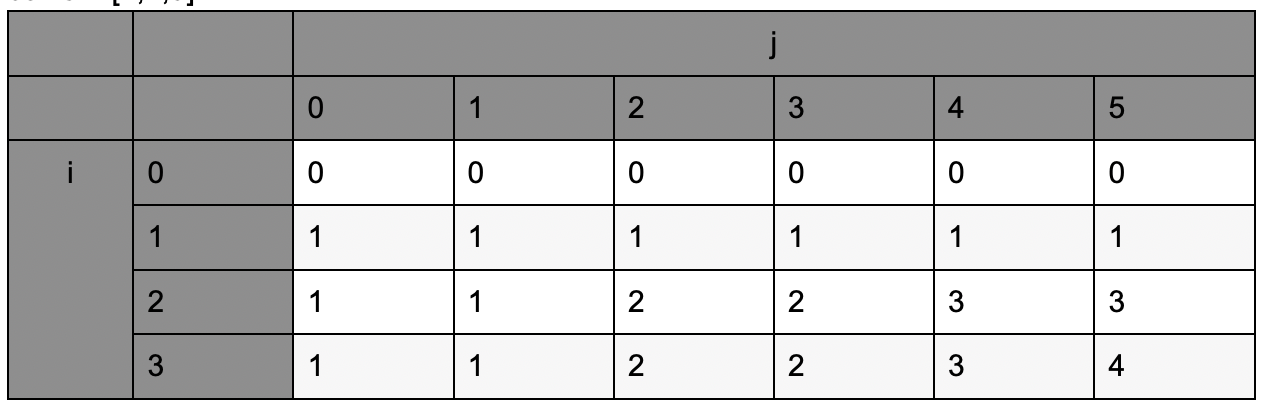
class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp = new int[coins.length + 1][amount + 1];

        for(int i = 1; i <= coins.length; i++){
            dp[i][0] = 1;                
            int currCoin = coins[i - 1];
            
            for(int j = 1; j <= amount; j++){
                // 少使用一种硬币组成当前 amount 组合数 + 使用当前的硬币组成当前 amount的组合数
                dp[i][j] = dp[i - 1][j];

                if(j >= currCoin) {
                    dp[i][j] += dp[i][j - currCoin];
                }
            }
        }

        return dp[coins.length][amount];
    }
}