356. Line Reflection

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

Given n points on a 2D plane, find if there is such a line parallel to y-axis that reflect the given points symmetrically, in other words, answer whether or not if there exists a line that after reflecting all points over the given line the set of the original points is the same that the reflected ones.

Note that there can be repeated points.

Follow up: Could you do better than O(n^2) ?

Example 1:

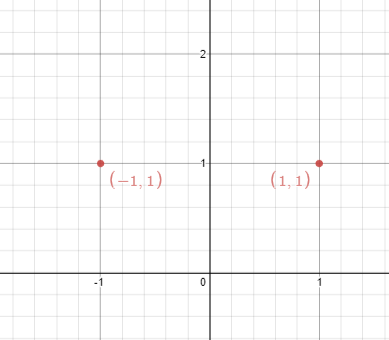
Input: points = [[1,1],[-1,1]]
Output: true
Explanation: We can choose the line x = 0.

Example 2:

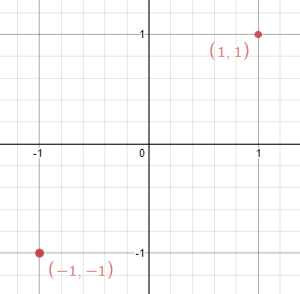
Input: points = [[1,1],[-1,-1]]
Output: false
Explanation: We can't choose a line.

Code

class Solution {
    public boolean isReflected(int[][] points) {
        HashSet<String> set = new HashSet<>();
        int min = Integer.MAX_VALUE;
        int max = Integer.MIN_VALUE;

        for(int[] point : points){
            set.add(point[0] +"," +point[1]);
            min = Math.min(min, point[0]);
            max = Math.max(max, point[0]);
        }

        int sum = min + max;

        for(int[] point : points){
            if(!set.contains(sum - point[0] + "," + point[1])){
                return false;
            }
        }

        return true;
    }
}