351. Android Unlock Patterns

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

Android devices have a special lock screen with a 3 x 3 grid of dots. Users can set an “unlock pattern” by connecting the dots in a specific sequence, forming a series of joined line segments where each segment’s endpoints are two consecutive dots in the sequence. A sequence of k dots is a valid unlock pattern if both of the following are true:

• All the dots in the sequence are distinct.
• If the line segment connecting two consecutive dots in the sequence passes through any other dot, the other dot must have previously appeared in the sequence. No jumps through non-selected dots are allowed. Here are some example valid and invalid unlock patterns:

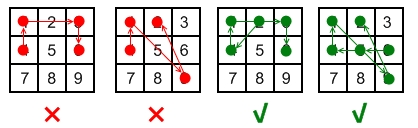
• The 1st pattern [4,1,3,6] is invalid because the line connecting dots 1 and 3 pass through dot 2, but dot 2 did not previously appear in the sequence.
• The 2nd pattern [4,1,9,2] is invalid because the line connecting dots 1 and 9 pass through dot 5, but dot 5 did not previously appear in the sequence.
• The 3rd pattern [2,4,1,3,6] is valid because it follows the conditions. The line connecting dots 1 and 3 meets the condition because dot 2 previously appeared in the sequence.
• The 4th pattern [6,5,4,1,9,2] is valid because it follows the conditions. The line connecting dots 1 and 9 meets the condition because dot 5 previously appeared in the sequence.

Given two integers m and n, return the number of unique and valid unlock patterns of the Android grid lock screen that consist of at least m keys and at most n keys.

Two unlock patterns are considered unique if there is a dot in one sequence that is not in the other, or the order of the dots is different.

Code

class Solution {
  public int numberOfPatterns(int m, int n) {
    int[][] skip = new int[10][10];
    // 记录要跳过的情况
    skip[1][3] = skip[3][1] = 2;
    skip[1][7] = skip[7][1] = 4;
    skip[3][9] = skip[9][3] = 6;
    skip[7][9] = skip[9][7] = 8;

    skip[1][9] = skip[9][1] = 5;
    skip[2][8] = skip[8][2] = 5;
    skip[3][7] = skip[7][3] = 5;
    skip[4][6] = skip[6][4] = 5;

    boolean[] visited = new boolean[10];
    int res = 0;

    for(int i = m; i <= n; i++){
      // 1,3,7,9对称
      // 已经用了一个点，所以要先i - 1
      res += dfs(visited, skip, 1, i - 1) * 4;
      // 2,4,6,8对称
      res += dfs(visited, skip, 2, i - 1) * 4;
      // 5
      res += dfs(visited, skip, 5, i - 1);
    }

    return res;
  }

  // remain 还剩下几个点可以用
  private int dfs(boolean[] visited, int[][] skip, int cur, int remain){
    if(remain < 0) return 0;
    if(remain == 0) return 1;

    visited[cur] = true;
    int res = 0;

    for(int i = 1; i <= 9; i++){
      // 节点还没有访问过 && (skip == 0表示相邻的点，不需要越过 ||
      // visited[skip[cur][i]]需要跳过，但是需要用的中介点已经访问过了)
      if(!visited[i] && (skip[cur][i] == 0 || visited[skip[cur][i]])){
        res += dfs(visited, skip, i, remain - 1);
      }
    }

    visited[cur] = false;
    return res;
  }
}