33. Search in Rotated Sorted Array

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

There is an integer array nums sorted in ascending order (with distinct values).

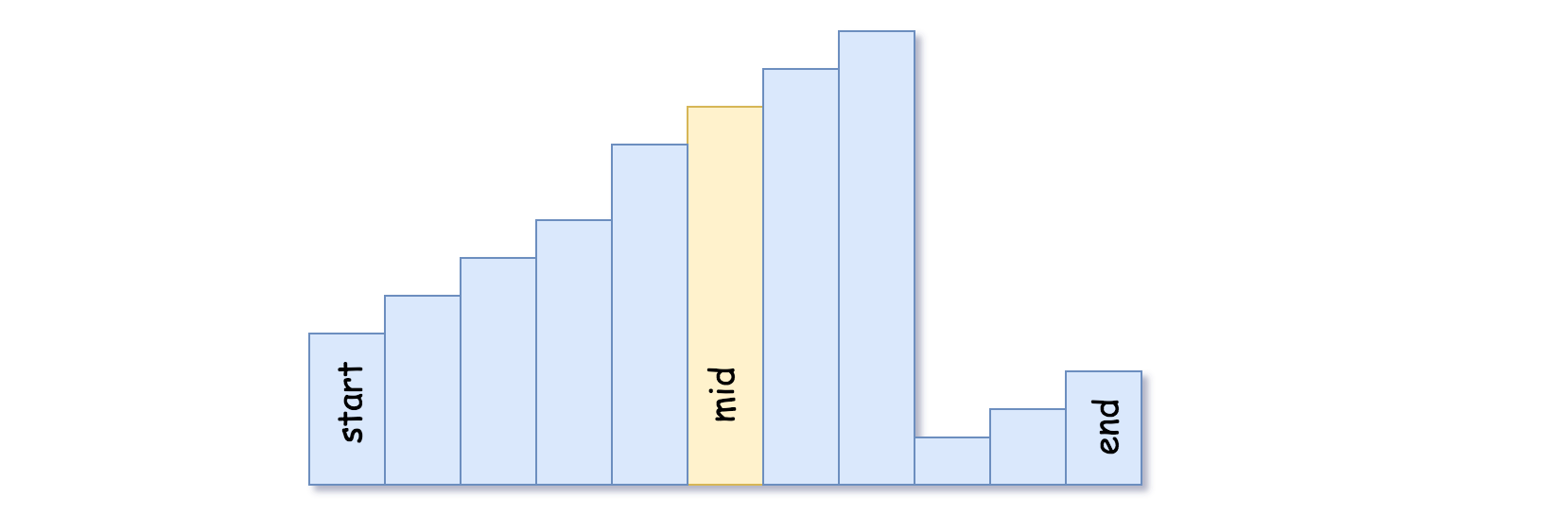
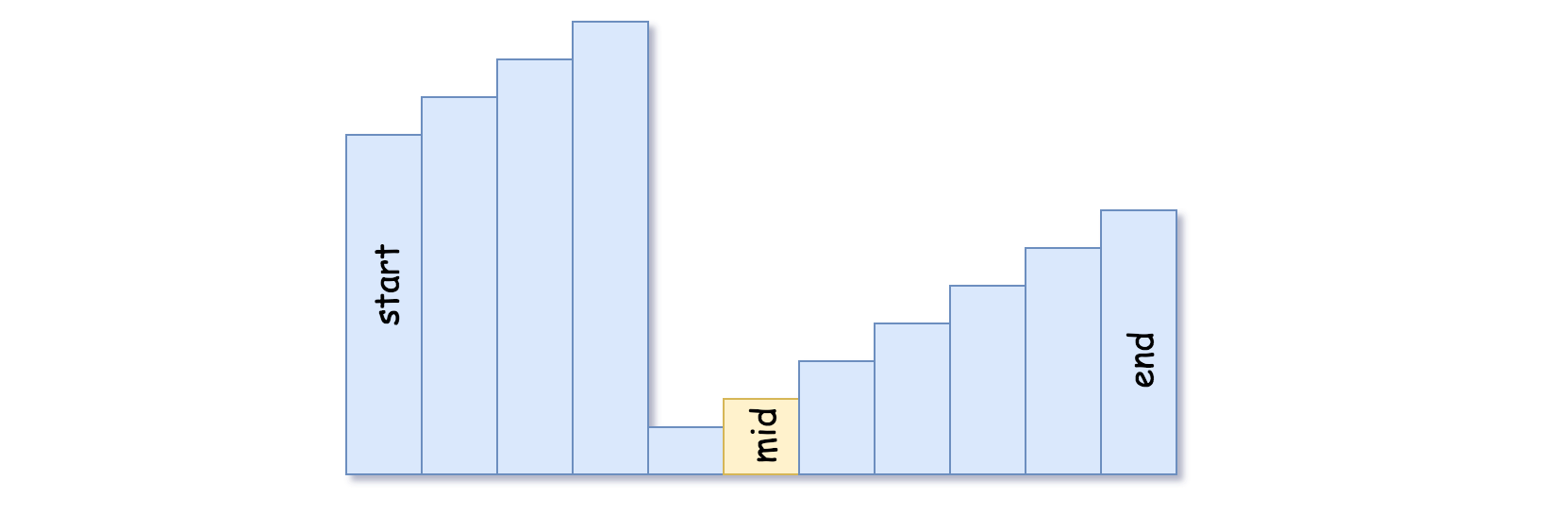
Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Example 3:

Input: nums = [1], target = 0
Output: -1

Constraints:

• 1 <= nums.length <= 5000
• $-10^4 <= nums[i] <= 10^4$
• All values of nums are unique.
• nums is an ascending array that is possibly rotated.
• $-10^4 <= target <= 10^4$

Code

class Solution {
    public int search(int[] nums, int target) {
        if(nums == null || nums.length == 0) return -1;

        int left = 0;
        int right = nums.length - 1;
        while(left + 1 < right){
            int mid = left + (right - left) / 2;
            if(nums[mid] == target) return mid;

            if(nums[left] <= nums[mid]){
                if(nums[left] <= target && target <= nums[mid]){
                    right = mid;
                } else {
                    left = mid;
                }
            } else {
                if(nums[mid] <= target && target <= nums[right]){
                    left = mid;
                } else {
                    right = mid;
                }
            }
        }

        if(nums[left] == target){
            return left;
        } else if (nums[right] == target){
            return right;
        } else {
            return -1;
        }
    }
}