261. Graph Valid Tree

JIAKAOBO

LeetCode

感谢赞助!

• ㊗️
• 大家
• offer
• 多多！

Problem

Given n nodes labeled from 0 to n-1 and a list of undirected edges (each edge is a pair of nodes), write a function to check whether these edges make up a valid tree.

Example 1:

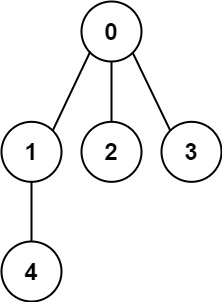
Input: n = 5, and edges = [[0,1], [0,2], [0,3], [1,4]]
Output: true

Example 2:

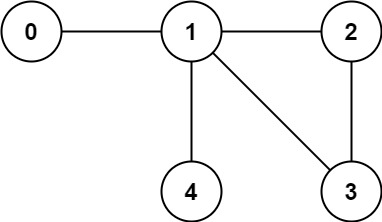
Input: n = 5, and edges = [[0,1], [1,2], [2,3], [1,3], [1,4]]
Output: false

Constraints:

• 1 <= n <= 2000
• 0 <= edges.length <= 5000
• edges[i].length == 2
• $0 <= a_i, b_i < n$
• $a_i != b_i$
• There are no self-loops or repeated edges.

Code

684. Redundant Connection

Union Find

class Solution {
    public class UnionFind {
        int[] parents;
        int[] ranks;

        public UnionFind(int n) {
            parents = new int[n];
            ranks = new int[n];

            for (int i = 0; i < n; i++) {
                parents[i] = i;
                ranks[i] = 1;
            }
        }

        public boolean union(int x, int y) {
            int xParent = find(x);
            int yParent = find(y);

            if (xParent == yParent) return false;

            if (ranks[xParent] > ranks[yParent]) {
                parents[yParent] = xParent;
            } else if (ranks[xParent] < ranks[yParent]) {
                parents[xParent] = yParent;
            } else {
                parents[yParent] = xParent;
                ranks[xParent]++;
            }

            return true;
        }

        public int find(int node) {
            if(node == parents[node]) return node;

            return find(parents[node]);
        }
    }

    UnionFind node;
    public boolean validTree(int n, int[][] edges) {
        // 注意孤立点
        // [0, 1], [2, 3] n = 4
        // 这种情况也不是树
        if(edges.length + 1 < n) return false;
        node = new UnionFind(n);

        for(int[] edge : edges){
            if(!node.union(edge[0], edge[1])){
                return false;
            }
        }

        return true;
    }
}

class UnionFind:
    def __init__(self, n: int):
        self.parents = [i for i in range(n)]
        self.ranks = [1] * n

    def union(self, u: int, v: int) -> bool:
        pu = self.find(u)
        pv = self.find(v)

        if pu == pv:
            return False

        if self.ranks[pu] > self.ranks[pv]:
            self.parents[pv] = pu
        elif self.ranks[pu] < self.ranks[pv]:
            self.parents[pu] = pv
        else:
            self.parents[pv] = pu
            self.ranks[pu] += 1

        return True

    def find(self, u: int) -> int:
        if self.parents[u] == u:
            return u

        return self.find(self.parents[u])

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        if len(edges) != n - 1:
            return False

        node = UnionFind(n)

        for edge in edges:
            if not node.union(edge[0], edge[1]):
                return False

        return True

// find 也可以写成下面的形式
public int find(int node) {
    while (node != parents[node]) {
        int parentNode = parents[parents[node]];
        node = parentNode;
    }

    return node;
}

Time Complexity: O(N⋅α(N)) Space Complexity: O(N)

DFS

class Solution {
    public boolean validTree(int n, int[][] edges) {
        if(n == 1) {
            return true;
        }

        HashMap<Integer, List<Integer>> graph = new HashMap<>();

        for(int[] edge : edges) {
            if(!graph.containsKey(edge[0])) {
                graph.put(edge[0], new ArrayList<>());
            }

            graph.get(edge[0]).add(edge[1]);

            if(!graph.containsKey(edge[1])) {
                graph.put(edge[1], new ArrayList<>());
            }

            graph.get(edge[1]).add(edge[0]);
        }

        HashSet<Integer> visited = new HashSet<>();
        visited.add(0);

        boolean res = helper(graph, visited, 0, -1);

        if(!res) {
            return false;
        }

        return visited.size() == n;
    }

    private boolean helper(HashMap<Integer, List<Integer>> graph, HashSet<Integer> visited, int curr, int parent) {
        if(!graph.containsKey(curr)) {
            return false;
        }
        List<Integer> subs = graph.get(curr);

        for(int sub : subs) {
            if(parent == sub){
                continue;
            }

            if(visited.contains(sub)){
                return false;
            }

            visited.add(sub);
            boolean res = helper(graph, visited, sub, curr);
            if(!res){
                return false;
            }
        }

        return true;
    }
}

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        # 1. 不会构成连通图
        # 2. 没有孤立的点
        graph = defaultdict(list)

        for edge in edges:
            graph[edge[0]].append(edge[1])
            graph[edge[1]].append(edge[0])

        visited = set()
        visited.add(0)

        res = self.helper(graph, visited, 0, -1)

        if not res:
            return False

        return True if len(visited) == n else False

    def helper(self, graph: List[List[int]], visited: Set[int], node: int, parent: int):
        subs = graph[node]

        for sub in subs:
            if sub == parent:
                continue

            if sub in visited:
                return False

            visited.add(sub)
            res = self.helper(graph, visited, sub, node)

            if not res:
                return False

        return True

Time Complexity : O(N + E) Space Complexity : O(N + E)