JIAKAOBO

LeetCode

venmo
wechat

感谢赞助!

  • ㊗️
  • 大家
  • offer
  • 多多！

Problem

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node’s values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

img

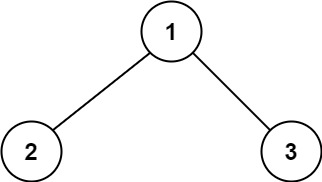
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

img

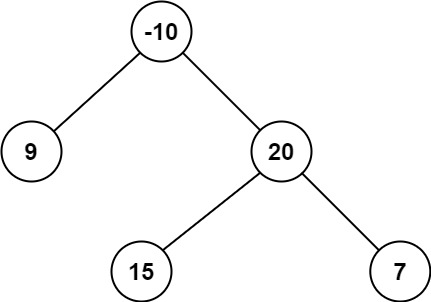
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

  • The number of nodes in the tree is in the range $[1, 3 * 10^4]$.
  • $-1000 <= Node.val <= 1000$

Code

class Solution {
    int res = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        helper(root);
        return res;
    }

    private int helper(TreeNode root){
        if(root == null) return 0;
        int left = Math.max(helper(root.left), 0);
        int right = Math.max(helper(root.right), 0);

        res = Math.max(res, left + right + root.val);

        return Math.max(left, right) + root.val;
    }
}